Understanding polygons is fundamental in geometry. A pentagon, a five-sided polygon, exemplifies geometric principles. The formula for calculating the sum of interior angles dictates what is the inner sum degrees in a pentagon? The inner sum of a pentagon equals 540 degrees which is a core concept taught in the Euclidean Geometry.
The pentagon, a five-sided polygon, is a foundational shape in geometry. It appears in various contexts, from everyday objects to complex architectural designs. Yet, despite its ubiquity, a surprisingly large number of people stumble when asked a fundamental question about it:
What is the sum of the interior angles in a pentagon?
The answer, while elegantly simple, often eludes casual recall. This introduction aims to not only provide that answer but also to explore the underlying geometric principles that make it so.
The Pentagon: A Brief Overview
At its core, a pentagon is a two-dimensional geometric figure defined by five straight sides and five vertices (corners). These sides connect to form five interior angles.
Pentagons can be regular, with all sides and angles equal, or irregular, where sides and angles vary in measure. Our primary focus here is on understanding a property applicable to all pentagons, regardless of their regularity: the sum of their interior angles.
The Question That Catches Many
"What is the inner sum degrees in a pentagon?" is a deceptively straightforward question. It taps into a basic geometric concept – the sum of interior angles in polygons.
While many might recall similar rules for triangles (180 degrees) or quadrilaterals (360 degrees), the pentagon’s value often proves more elusive.
The Simplicity Often Overlooked
The beauty of geometry lies in its inherent logic and order. The sum of the interior angles of a pentagon isn’t some arbitrary number. It’s a direct consequence of geometric theorems and can be easily derived.
The fact that this simple concept is often overlooked highlights a common challenge in mathematics education: remembering formulas without truly understanding their origins. This exploration will emphasize that understanding, revealing the straightforward calculation behind the pentagon’s angle sum.
The beauty of geometry lies in its inherent logic and order. The sum of the interior angles of a pentagon isn’t some arbitrary number. It’s a direct consequence of geometric theorems and can be easily understood by first establishing the fundamental building blocks of this fascinating shape.
Pentagon Fundamentals: Sides, Vertices, and Angles
Before diving into the calculation of interior angles, it’s crucial to solidify our understanding of what constitutes a pentagon. This involves defining its key components: sides, vertices, and angles.
Defining the Pentagon: Sides and Vertices
At its most basic, a pentagon is a closed, two-dimensional shape formed by five straight line segments, or sides. These sides connect at five points, known as vertices, or corners.
Think of it like a five-sided figure drawn without lifting your pen, ensuring the starting point meets the ending point. The number of sides and vertices are always equal in a pentagon.
Interior vs. Exterior Angles
Every vertex in a pentagon forms two types of angles: interior and exterior. The interior angle is formed inside the pentagon by two adjacent sides. Conversely, an exterior angle is formed by one side and the extension of an adjacent side.
Visualize extending one side of the pentagon beyond its vertex. The angle formed between this extension and the adjacent side is the exterior angle.
For our purposes, we will concentrate primarily on the interior angles, as they are the key to answering our central question.
Degrees: The Unit of Measurement
Angles are measured in degrees, symbolized by the (°). A full circle contains 360 degrees. A straight line forms an angle of 180 degrees.
Understanding this unit is essential. It allows us to quantify the "amount of turn" at each vertex of the pentagon and, ultimately, determine the sum of all its interior angles.
The journey through sides, vertices, and angles provides the essential groundwork. Now, we arrive at the core of our exploration: the numerical value that represents the sum of a pentagon’s interior angles. It’s time to unveil this key piece of geometric knowledge.
The Inner Sum Revealed: 540 Degrees
The moment of truth has arrived. What is the sum of the interior angles within a pentagon? The answer, definitively, is 540 degrees. This single number encapsulates a fundamental property of this geometric shape.
Decoding the Sum of Angles Formula
How do we arrive at this precise figure? The sum of the interior angles of any polygon can be calculated using a simple yet powerful formula:
(n – 2)
**180
Where ‘n’ represents the number of sides the polygon has.
This formula isn’t arbitrary; it’s rooted in geometric principles that we’ll explore later.
Applying the Formula to a Pentagon
Let’s put this formula into action for our pentagon. A pentagon, by definition, has five sides (n = 5). Substituting this value into the formula:
(5 – 2)** 180
Simplifies to:
3 * 180 = 540
The Definitive Answer: 540 Degrees
Therefore, as stated earlier, the sum of the interior angles of a pentagon is unequivocally 540 degrees.
This value holds true for all pentagons, regardless of their size or shape.
Angle Sum Theorem: The Proof Behind the Number
The established fact that a pentagon’s interior angles sum to 540 degrees raises a crucial question: why is this true? Beyond the formula, a more fundamental principle underpins this geometric reality. That principle is the Angle Sum Theorem.
Unveiling the Angle Sum Theorem
The Angle Sum Theorem provides a rigorous justification for calculating the sum of interior angles in polygons. It posits that the sum of the interior angles of any triangle is always 180 degrees.
This seemingly simple statement is the cornerstone of polygon angle calculations. By strategically dividing a polygon into triangles, we can leverage this theorem to find the total sum of its interior angles.
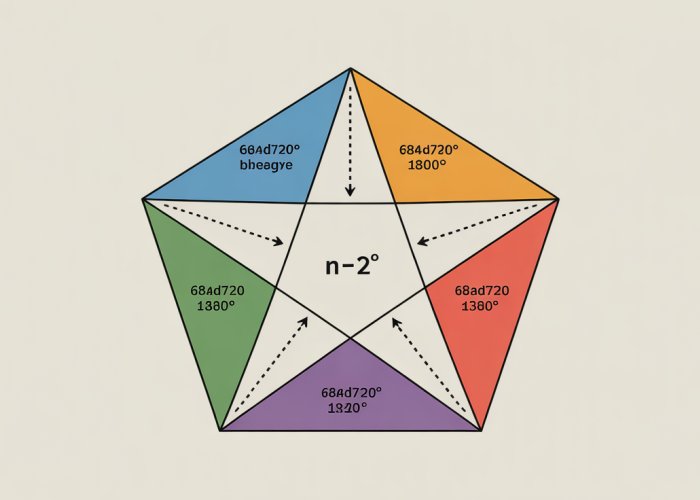
Triangulating the Pentagon
To apply the Angle Sum Theorem to a pentagon, the key is to decompose the pentagon into triangles. This is achieved by drawing diagonals from a single vertex to all non-adjacent vertices.
A pentagon can be divided into three triangles in this way. Since each triangle contributes 180 degrees to the total angle sum, the pentagon’s interior angles must sum to 3 * 180 = 540 degrees.
Linking Triangles to the Pentagon’s Interior Angle Sum
Each interior angle of the pentagon is now part of an individual triangle within the shape. The sum of the angles in the three triangles that form the pentagon represents the sum of all the interior angles of the pentagon itself.
Therefore, the Angle Sum Theorem for triangles elegantly explains why the sum of a pentagon’s interior angles is invariably 540 degrees. It demonstrates how a fundamental property of triangles extends to more complex polygons.
Deeper Understanding of Geometric Proof
This triangulation method isn’t limited to pentagons; it’s a general technique applicable to all polygons. By understanding this underlying principle, we gain a deeper appreciation for the elegance and interconnectedness of geometric theorems.
The Angle Sum Theorem exemplifies the power of breaking down complex shapes into simpler components to reveal their inherent properties. This theorem offers a powerful proof that goes beyond mere calculation. It showcases the fundamental geometric relationships that define the pentagon.
The Power of Formulas: Geometry’s Toolkit
Having established the principles governing the interior angles of a pentagon, it’s crucial to recognize that this understanding is built upon a foundation of geometric formulas. These formulas are not merely computational tools; they are the keys that unlock a deeper comprehension of shapes and their properties.
Formulas as Geometric Blueprints
Mathematical formulas in geometry serve as essential blueprints. They provide a structured framework for understanding the relationships between different elements of a shape.
Formulas act as succinct representations of geometric truths, allowing us to move beyond mere observation to precise calculation and prediction.
Unveiling Hidden Properties
One of the most significant roles of formulas is their ability to reveal hidden properties within geometric figures. They allow us to determine areas, volumes, surface areas, and angle measures.
These calculations are not limited to simple shapes like pentagons, triangles, and squares. Formulas allow us to analyze complex polyhedra, curves, and transformations with accuracy.
Formulas empower us to explore the inherent characteristics of geometric objects, leading to discoveries that would be impossible through visual inspection alone.
Beyond the Pentagon: A Universal Language
The application of geometric formulas extends far beyond the specific case of the pentagon. These formulas form a universal language for describing and analyzing the geometric world around us.
They are fundamental in fields such as architecture, engineering, computer graphics, and physics.
The principles that govern a pentagon’s angles also apply, with appropriate adaptations, to polygons with any number of sides. This scalability makes formulas invaluable for solving a wide range of geometric problems.
Geometry’s Foundation
Understanding formulas is not just about memorization; it’s about grasping the underlying principles that govern geometric space. These principles are the foundation upon which more advanced geometric concepts are built. They empower us to not only understand the properties of individual shapes, but also the relationships between them, and the ways in which they can be manipulated and transformed.
FAQs About The Pentagon’s Inner Sum
Here are some frequently asked questions about understanding the inner sum of a pentagon, and the "simple secret" to calculating it.
What exactly does "inner sum" refer to in this context?
"Inner sum" refers to the sum of the interior angles of a pentagon, that is, the angles formed inside the shape at each of its five vertices. A key concept to grasp is what is the inner sum degrees in a pentagon.
What’s the simple secret to easily find the inner sum of any pentagon?
The secret lies in understanding the formula (n-2) 180, where ‘n’ is the number of sides. Since a pentagon has 5 sides, the calculation is (5-2) 180 = 540 degrees. Understanding this eliminates the need to measure each angle individually.
Why is the inner sum of all pentagons always the same, regardless of their shape?
The sum of the interior angles depends only on the number of sides. All pentagons have 5 sides. Therefore, regardless of whether the pentagon is regular or irregular, convex or concave, what is the inner sum degrees in a pentagon will be 540°.
How is knowing the inner sum of a pentagon useful?
Knowing the total sum of the angles helps in various calculations. For example, in a regular pentagon where all angles are equal, you can divide 540° by 5 to find the measure of each interior angle (108°). This understanding is essential in geometry and design applications. What is the inner sum degrees in a pentagon is a fundamental building block.
So, there you have it! Knowing what is the inner sum degrees in a pentagon? is simpler than you might’ve thought. Now go impress your friends with your newfound geometric knowledge!



