Transverse waves, fundamental phenomena studied extensively in physics classrooms and by organizations like the Acoustical Society of America, exhibit a unique characteristic: oscillations perpendicular to the direction of propagation. These waves, measurable using tools like oscilloscopes, demonstrate varied speeds influenced by medium properties. Understanding transverse waves what speed is, therefore, critical in analyzing various phenomena, from light waves to the motions studied by pioneers like Lord Rayleigh.
Unlocking the Secrets: Transverse Waves and What Speed Reveals!
This article explores the fascinating world of transverse waves and how their speed provides valuable insights into their behavior and the medium through which they travel. We’ll delve into the key characteristics of these waves, the factors influencing their speed, and the implications of understanding this relationship.
What are Transverse Waves?
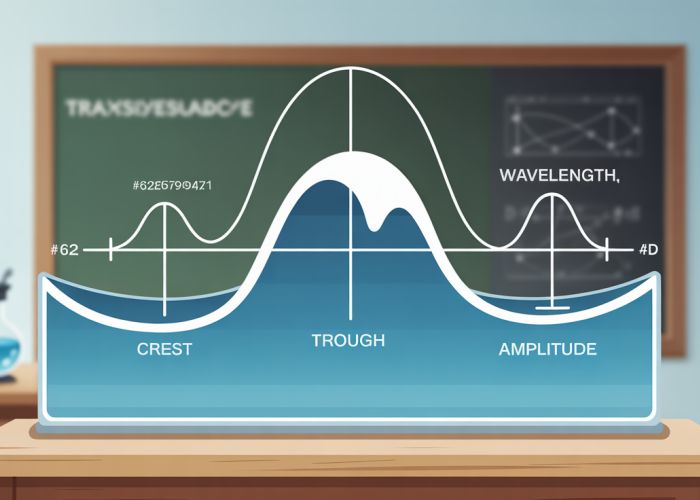
Transverse waves are characterized by the oscillation of particles perpendicular (at a right angle) to the direction the wave is moving. Imagine shaking a rope up and down. The wave travels along the rope, but the rope itself moves vertically, not along the direction of the wave.
- Key characteristics of transverse waves:
- Crests: The highest points of the wave.
- Troughs: The lowest points of the wave.
- Amplitude: The maximum displacement of a particle from its resting position. Think of it as the height of the crest (or depth of the trough).
- Wavelength (λ): The distance between two successive crests (or troughs).
- Frequency (f): The number of complete wave cycles that pass a given point per unit of time, usually measured in Hertz (Hz).
The Speed of Transverse Waves: A Crucial Indicator
The speed (v) of a transverse wave is determined by the properties of the medium it’s traveling through. Understanding wave speed allows us to infer important information about the medium itself. The relationship between speed, frequency, and wavelength is fundamental:
v = fλ
Where:
- v = wave speed
- f = frequency
- λ = wavelength
The Relationship Between Wave Speed, Frequency and Wavelength:
| Variable | Symbol | Units | Description |
|---|---|---|---|
| Wave Speed | v | meters/second (m/s) | How fast the wave is propagating through the medium. |
| Frequency | f | Hertz (Hz) | The number of wave cycles per second. |
| Wavelength | λ | meters (m) | The distance between two identical points on successive waves. |
This simple equation highlights that the speed of a wave is directly proportional to both its frequency and wavelength. If the frequency increases and the wavelength remains constant, the speed also increases. Similarly, if the wavelength increases and the frequency remains constant, the speed increases.
Factors Affecting the Speed of Transverse Waves
The material through which a transverse wave travels significantly influences its speed. Different materials offer varying levels of resistance or support to the wave’s propagation.
Waves on a String (or Rope)
The speed of a transverse wave on a string is determined by two main factors:
- Tension (T): The force with which the string is stretched. Higher tension generally results in a faster wave speed.
- Linear Density (μ): The mass per unit length of the string. A heavier string (higher linear density) generally results in a slower wave speed.
The equation describing this relationship is:
v = √(T/μ)
Waves in a Solid
In solid materials, the speed of a transverse wave (specifically a shear wave) depends on:
- Shear Modulus (G): A measure of the material’s rigidity or resistance to deformation when subjected to a shear stress (a force applied parallel to a surface). A higher shear modulus indicates a stiffer material and generally leads to a faster wave speed.
- Density (ρ): The mass per unit volume of the material. A denser material generally results in a slower wave speed.
The relationship is expressed as:
v = √(G/ρ)
Analyzing Medium Properties Through Wave Speed:
By measuring the speed of a transverse wave in a material and knowing some of its other properties, we can infer information about its characteristics. For example:
- String Tension: If we know the speed of a wave on a string and the linear density, we can calculate the tension in the string.
- Material Rigidity: Knowing the speed of a shear wave and the density of a solid, we can determine its shear modulus, giving us an idea of its stiffness.
- Detecting Changes: Changes in wave speed within a medium can indicate changes in the medium’s properties (e.g., temperature changes affecting density, or the presence of cracks in a solid affecting its shear modulus). This is used in applications such as medical imaging and non-destructive testing.
FAQs: Understanding Transverse Wave Speed
These frequently asked questions clarify some key concepts about transverse waves and their speed.
What factors influence the speed of a transverse wave on a string?
The speed of a transverse wave on a string depends on two main factors: the tension in the string and the mass per unit length of the string (linear density). Higher tension leads to a higher speed, while higher linear density results in a slower speed. This relationship determines transverse waves what speed.
How is the speed of a transverse wave related to its frequency and wavelength?
The speed of a transverse wave is directly related to its frequency and wavelength. The relationship is described by the equation: speed = frequency x wavelength. So, if you know the frequency and wavelength, you can easily calculate transverse waves what speed.
Why is understanding transverse waves what speed important?
Understanding the speed of transverse waves allows us to predict how they will propagate through a medium. This has implications in various applications, from musical instruments (string vibrations) to telecommunications (electromagnetic waves).
Does the amplitude of a transverse wave affect its speed?
No, the amplitude of a transverse wave does not affect its speed. The speed of transverse waves what speed on a string, for example, is solely determined by the tension and linear density of the string, regardless of how large the wave’s displacement is.
So, hopefully, you’ve unlocked some secrets regarding transverse waves what speed! Keep experimenting, keep observing, and keep those waves rocking!



